3 解析解

解析解は、Gastineら[の導出した式を元にOctaveを用いて数値解を求めた。 Gastineらの導出した式は、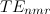 $TE_{nmr}$ モードに関して、

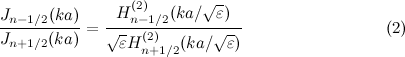$\begin{equation} \frac{J_{n-1/2}(ka)}{J_{n+1/2}(ka)} = \frac{H^{(2)}_{n-1/2}(ka/\sqrt {\varepsilon })}{\sqrt {\varepsilon }H^{(2)}_{n+1/2}(ka/\sqrt {\varepsilon })} \label{eq:gastine_ te} \end{equation}$

(2)

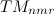である。また、 $TM_{nmr}$ モードに関して、

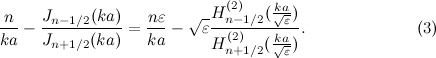$\begin{equation} \frac{n}{ka} - \frac{J_{n-1/2}(ka)}{J_{n+1/2}(ka)} = \frac{n\varepsilon }{ka} - \sqrt {\varepsilon } \frac{H^{(2)}_{n-1/2}(\frac{ka}{\sqrt {\varepsilon }})}{H^{(2)}_{n+1/2}(\frac{ka}{\sqrt {\varepsilon }})}. \label{eq:gastine_ tm} \end{equation}$

(3)

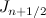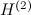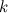ただし、 $J_{n+1/2}$ は第一種ベッセル関数、 $H^{(2)}$ は第二種ハンケル関数であり、誘電体球の半径を $a$ 、比誘電率を $\varepsilon$ とする。また、 $k$ は動径方向の波数である。与えられた 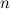$n$ に対して、式(),()を満たす 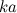$ka$ が共鳴の固有解となる。

これらの式の解をOctaveを用いてNewton-Raphson法によって求解したのが表 1, である。

n	Hz
1	2.3161 $\times 10^{8}$
2	3.3481 $\times 10^{8}$
3	4.3117 $\times 10^{8}$
4	5.2364 $\times 10^{8}$

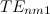Table 1: $TE_{nm1}$ モードでの共鳴周波数。mに関しては縮退している。r に関しては基本モードのみ求めている。

n	Hz
1	3.2638 $\times 10^{8}$
2	4.2721 $\times 10^{8}$
3	5.2086 $\times 10^{8}$
4	6.1140 $\times 10^{8}$

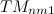Table 2: $TM_{nm1}$ モードでの共鳴周波数。mに関しては縮退している。r に関しては基本モードのみ求めている。